Created Wednesday 16 October 2024
I never learned General Relativity, so I don't really know how to imagine a curved 4-dimensional space-time with Minkowski metric — but I can certainly imagine a sphere, as an example of a curved 2-dimensional space. So I thought I'd start from sphere and half-guess, half-learn how wormholes work. Ha.
Sphere seemed like a great example, because it has the main symmetries of our conventional space: it is uniform and isotropic (every point of a sphere is exactly the same as any other point, and any direction is the same as any other direction) From my vague memories of a course in theoretical mechanics, this should mean that the laws of the conservation of momentum and of angular momentum will hold.
Naively, I also thought that the Galilean relativity will also apply: a reference frame moving at a constant velocity will be indistinguishable from a stationary one. But that is not at all true! A body moving freely on a sphere will follow the big circle, like an equator or a meridian on Earth. Tow bodies originally moving in parallel will start drifting closer to each other, and will eventually meet, after travelling the distance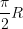 
where R is the radius of the sphere. Put it another way, a rigid body moving freely on a sphere will experience a force, squeezing it in the direction orgthogonal to the direction of motion. If you are on a sphere, you can always tell if you are moving or if you are stationary!
P.S.: Technically, this is not the same as spaghettification. When you are falling into a black hole, you simultaneously experience a force squeezing you in the directions orgthogonal to the direction towards the black hole, and stretching you in the direction towards and away from the black hole. In the case of a moving body on a sphere, you are only squeezed. But in both cases, it is a force caused by the curvature of the space(-time).